The artificial neural network cost function helps machine learning system learn from their mistakes.


In a previous article, Neural Network Backpropagation, I define backpropagation as a machine-learning technique used to calculate the gradient of the cost function at output and distribute it back through the layers of the artificial neural network, providing guidance on how to adjust the weights of the connections between neurons and the biases within certain neurons to increase the accuracy of the output.
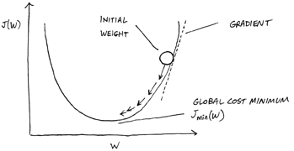
Imagine backpropagation as creating a feedback loop in the neural network. As the machine tries to match inputs to labels, the cost function tells the neural network how wrong its answer is. Backpropagation then feeds the error back through the network to make adjustments via gradient descent —an optimization algorithm that minimizes cost by repeatedly and gradually moving the output in the direction where the slope of the gradient decreases, as shown below. The goal is to reach the global cost minimum — the point where the slope of the gradient is as close to zero as possible.
Backpropagation relies on the neural network chain rule — a technique used to find the derivatives of cost with respect to any variable in a nested equation. In math, a derivative expresses the rate of change at any given point on a graph; it is the slope of the tangent at that point. A tangent is a line that touches a curve at only one point. As shown in the image above, the dotted line labeled "Gradient" and the solid line labeled "Global Cost Minimum" both represent tangents; their slopes represent derivatives.
Note that gradient descent gradually moves the weight of a connection from a point where the slope of the tangent is very steep to a point where the slope is nearly flat. The chain rule can be used to calculate the derivative of cost with respect to any weight in the network. This enables the network to identify how much each weight contributes to the cost (and causes the wrong answer) and whether that weight needs to be increased or decreased (and by how much) to reduce the cost (and improve the odds of a right answer).
Here's how the cost function, the chain rule, gradient descent, and backpropagation of errors work together to enable the neural network to learn:
With backpropagation, weights and biases are adjusted from the output layer back through the hidden layers to the input layer. For example, if the neural network has four layers — an input layer, an output layer, and two hidden layers — weights and biases are adjusted in the following order:
In other words, the network turns the dials, starting with the dials closest to the output and working back through the network, testing the output after every adjustment and before making the next adjustment.
Using this technique, the network is able to reduce errors by fine-tuning the weights and biases one level at a time.
Through the chain rule, backpropagation focuses less on individual adjustments and more on the cumulative effect of those adjustments. Therefore, it uses the following strategies to make adjustments:
As you work with artificial neural networks and machine learning, keep in mind that no one factor is responsible for learning. Several elements must work together, including the cost function, the chain rule, gradient descent, and backpropagation of errors. Machine learning is essentially an exercise in testing answers and nudging the entire network toward reducing the likelihood of wrong answers.
The artificial neural network cost function helps machine learning system learn from their mistakes.
The perceptron history starts with Frank Rosenblatt and the earliest work on artificial neural networks. This was some of the earliest steps in artificial intelligence.
Machine learning gradient descent helps machines see how far off they are from making accurate predictions. Then the machine learning algorithm to tweak the learning model.