An artificial neural network is a type of machine learning that takes input and recognizes patterns then makes a decision or predication about the output.


An artificial neural network is a machine learning system made up of numerous interconnected neurons arranged in layers to simulate the structure and function of a biological brain. Learning occurs in a biological brain, in part, by the strengthening of connections between neurons. When you are learning a new subject or a new skill, the neurons in your brain form new connections with other neurons. The more you study or practice, the stronger these connections become.
In an artificial neural network, learning occurs in a similar fashion:
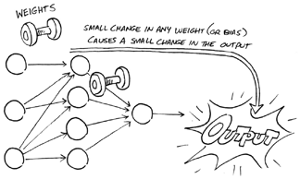
Each node in an artificial neural network has an activation function that performs a mathematical operation on the sum of its weighted inputs and bias and produces an output. (A function is a special relationship in which each input has a single output.)
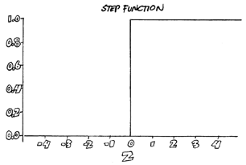
Different functions produce different outputs, and when you graph the outputs, you get different shapes. The most basic function used in machine learning is the Heaviside step function. This function outputs 1 (one) if its weighted input plus bias is positive or zero, and it outputs 0 (zero) if its weighted input plus bias is negative. In other words, the neuron either fires or doesn't. When you graph this function, you get something that looks like a step in a stairway, as shown below. The output can be one or zero, nothing in between.
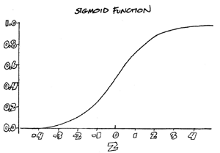
The sigmoid function provides infinitely more variation in values than you get with a binary function like the Heaviside step function. When graphed, output from a sigmoid function forms an "S" shape, as shown below. Sigmoid functions are commonly used in neural networks because they allow for making small adjustments within a limited range (0.0 to 1.0 on the vertical access) during the machine learning process.
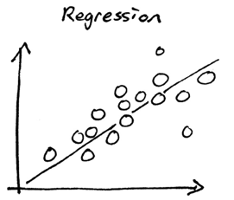
Note that regression functions, which are also used in machine learning, are not as useful in an artificial neural network, because their output range is infinite. The narrow range of a sigmoid function (from 0.0 to 1.0 on the vertical axis) makes the model more efficient and stable.
Weights enable the artificial neural network to dial up or dial down connections between neurons. For example, suppose you create an artificial neural network to distinguish among different dog breeds. Each neuron in one layer of the neural network may focus on a different characteristic — snout, ears, eyes, tail, size, shape, color, and so on. With weighted inputs, the network can increase or decrease the strength of the connection between each neuron in this layer and the neurons in the next layer to place less emphasis on the tail, for example, and more on the size and shape.
While weights enable an artificial neural network to adjust the strength of connections between neurons, bias can be used to make adjustments within neurons. Bias can be positive or negative, increasing or decreasing a neuron’s output. The neuron gathers and sums its inputs, adds bias (positive or negative) and then passes the total to the activation function.
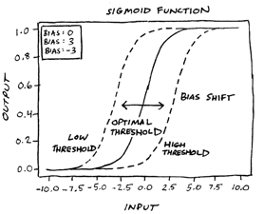
In terms of the sigmoid function graph presented earlier in this chapter, weight impacts the steepness of the curve, while bias shifts the curve left or right without changing the shape of the curve.
A cost function or loss function indicates the accuracy of the model. Its output tells the neural network whether weights and biases need to be adjusted to improve the model's accuracy. Think of the cost function as the means to reward the machine for success and/or punish it for failure. It enables the machine to learn from its achievements or mistakes.
To understand the interaction of functions, weights, and biases, imagine a neural network as a sound system with various dials for adjusting different parameters — volume, tone, balance, and so on. During the machine learning process, a neural network may turn dozens, hundreds, or even thousands of dials, making tiny adjustments to weights and biases, and then checking the end result. It repeats this process over and over to optimize the output's accuracy with every iteration.
An artificial neural network is a type of machine learning that takes input and recognizes patterns then makes a decision or predication about the output.
Deep learning is a machine learning technique that creates an artificial neural network that is many layers "deep."
The neural network chain rule works with backpropagation to help calculate the cost of the error in the gradient descent.